در پست قبلی راجع به مقدمه‌ای از نظریه بازی‌ها صحبت کردیم و مثال معروف زندانی‌ها را باهم بررسی کردیم. در این مقاله سعی میکنیم تا پیرامون پایه و اساس مسائل نظریه بازی صحبت کنیم و نحوه پیاده سازی مسائل مختلف با اِلِمان های نظریه بازی را یاد میگیریم.

مسائل بازی‌ها انواع و اقسام مختلفی دارند و طیف گسترده‌ای از موضوعات مختلف را در زمینه‌های مختلف شامل میشوند، با این حال همه مسائل را میتوان به سه قسمت تقسیم کرد:

•  Players(عامل ها): تکنیکالی واضح‌ترین بخش هر بازی عامل‌های(بازیکنان) آن هستند. در نظریه بازی، بازیکنان کسانی(یا مولفه هایی) هستند که در هر حالت (state) تصمیم گیرنده هستند، آنها میتوانند مردم عادی در مسائل روزمره باشند یا دولتمردان چند کشور که مذاکراتی را برای مسائل بازرگانی با یکدیگر انجام میدهند و یا چند شرکت تجاری در یک حوزه خاص که بدنبال استراتژی هایی برای توسعه و فروش محصولات خود هستند.
• Actions: منظور مجموعه انتخاب‌ها یاتصمیم‌هایی که هر عامل میتواند در بر داشته باشد. actionها بسته به نوع هر مسئله و شرایط تصمیم گیری هر عامل متفاوت است. مثلا در هنگام شرکت در یک مزایده تصمیم هر عامل میزان قیمت پیشنهادی در طرح مربوطه است یا در بورس میتوان تصمیم گیری را میزان خرید/فروش یک سهام و زمان انجام این کار دانست یا در بازی شطرنج انتخاب هر بازیکن در هر مرحله برابر تمامی حرکت های ممکن فرد در آن لحظه از بازی است.
• payoff (عایدی): انگیزه هر عامل برای شرکت کردن در بازی عایدی آن را تعیین خواهد کرد. عایدی هر عامل عبارت است از سودی که هر عامل در انتهای بازی نصیبش میشود که میتواند برنده شدن یا نشدن در یک بازی و یا مقادیری مانند میزان سود یک شرکت پس از اعمال تصمیم‌ها(Actions) باشد.

حتما همه‌ی شما با بازی tic tac toe یا همان دوز آشنایی دارید (اگر ندارید اینجا را ببینید) بازی که دو بازیکن برای سه‌تایی کردن مهره هایشان در یک جدول سه در سه تلاش میکنند، در این بازی دو بازیکن(Player) به نام‌های X و Y هستند و Action هر بازیکن انتخاب یک خانه خالی بین خانه‌های موجود هست و عایدی هر بازکن هم برنده شدن یا بازنده شدن و یا مساوی میباشد.

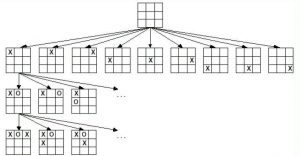
 در جدول بالا در درختی از حالت های بازی دوز را شاهد هستیم در هر مرحله یک بازیکن یکی از خانه های خالی را انتخاب میکند و در مرحله بعد بازیکن دیگری (هر گزینه) حالت های ممکن را انتخاب میکند و همینطور بازی پیش میرود، فرض کن در قسمتی از درخت به حالت زیر رسیدیم.

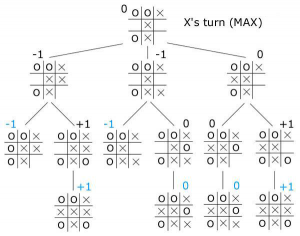
x در اینجا ۳ انتخاب دارد و پس از آن هم نوبت Y هست . ادامه بازی(اعدادی که میبینید مثبت یک برابر با برد  X و صفر برابر مساوی شدن و منفی یک برابر با باختن X است).

مبحث این قسمت ما تمام شده است اما اگر با دقت بیشتری به درخت نگاه کنیم متوجه خواهیم شد که با استفاده ای آخرین فرزند هر شاخه و پیمایش آن به سمت بالا متوجه خواهیم شد که اگر Y بهترین بازی خود را انجام دهد، X در چه صورتی حتما برنده خواهد شد(از پایین به بالا نگاه کنید!). در مقاله بعدی راجب ساختن درخت با استفاده از شبه کد و الگوریتم برد هر بازیکن و البته پر کردن درخت با جزییات تمام صحبت میکنیم و کاربرد نظریه بازی را از نزدیک لمس خواهیم کرد.

پیروز و موفق باشید.