درخت دودویی

درخت دودویی
درختی که هر گره از آن حداکثر دو فرزند داشته باشد. به عبارت دیگر درختی که درجه آن دو باشد درخت دودویی نامیده می شود. در درخت های معمولی ترتیب گره ها مهم نیست اما در درخت دودویی ترتیب گره ها دارای اهمیت است.
حداكثر تعداد گره ها در سطح i ام يک درخت دودويی 2i-1 بوده و حداكثر تعداد گره ها در يک درخت دودويی به عمق 2k-1 ،k است (درخت دودویی پر).
در درخت های دودویی در صورتی که تعداد گره ها را با n، تعداد گره های درجه صفر را با n0، تعداد گره های درجه یک را با n1، تعداد گره های درجه دو را با n2 نمایش دهیم در این صورت روابط زیر برقرار است.
حداقل تعداد گره های لازم برای ساختن درختی با ارتفاع h، h+1 گره است. مثل شکل زیر:
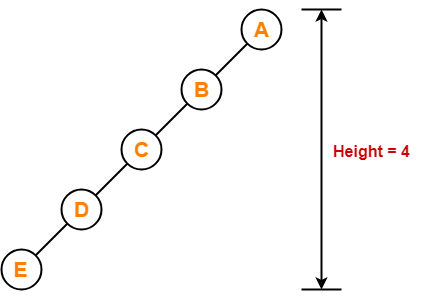
برای ساختن درختی به ارتفاع چهار دست کم به پنج گره احتیاج داریم
ارتفاع یک درخت دودویی کامل با n گره برابر ⎤(log2(n +1⎡ است.
بیشترین تعداد گره در سطح L ام یک درخت دودویی برابر است با :2L.
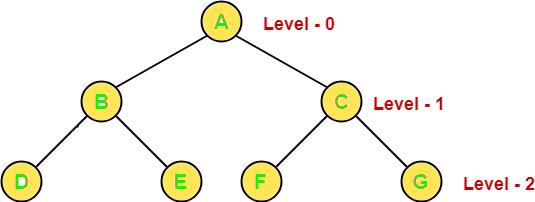
بیشترین تعداد گره ممکن در هر سطح درخت دودویی
حداكثر تعداد گره ها در يك درخت دودویی با ارتفاع h برابر است با :2h + 1 – 1.
بیشترین تعداد گره برای درختی با ارتفاع 4 برابر است با: 1-25 = 1-32 =31
برای هر درخت دودویی در صورتی که درخت تهی نباشد تعداد گره های پایانی همواره یکی بیشتر از تعداد گره هایی است که دارای دو فرزند هستند.
نمایش درخت دودویی به وسيله آرايه
یک درخت دودویی كامل با n گره را مي توان در يک آرايه يک بعدی ذخيره كرد.
برای ذخیره کردن یک درخت دودویی به این صورت عمل می کنیم:
گره های درخت شماره گذاری می شوند. شماره گذاری به ترتيب از بالا به پايين و از چپ به راست انجام می گردد و به هر گره شماره ای نسبت داده می شود. سپس گره با شماره i در خانه i آرايه قرار داده می گیرد.
در نمایش درخت دودویی به کمک آرایـــه برای گره i:
• ريشه درخت در گره 1 است.
• اگر i ≠1 باشد، پدر i در (i / 2) است و اگر i = 1 باشد i ريشه است.
• اگر 2i ≤ n باشد فرزند چپ i در 2i است در غیر این صورت گره فرزند چپ ندارد.
• اگر 2i+1 ≤ n باشد، فرزند راست i در 2i+1 است، در غیر این صورت گره i فـــاقد فرزند راست است .
این روش برای نمایش درختان غیر کامل زیاد مناسب نیست چون بسیاری از خانه های آرایه خــــالی باقی می ماند، در نتیجه بهتر است برای درختانی بجز درخت های پُر و کامل از نمایش با اشاره گر استفاده کنیم. در بدترين حالت، یک درخت مورب به عمق k، به 2k –1 محل و موقعيت نياز دارد كه از اين مقدار، فقط k محل اِشغال می شوند. در اين روش، درج و حذف گره ها نياز به جابجا کردن گره های دیگر دارد و این عامل موجب كــــند شدن عملیات درج و حــذف می شود.
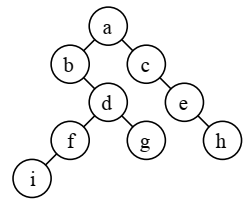
نمایش درخت دودویی با کمک آرایه
|
20 |
19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| i | h | g | f | e | d | c | b |
a |
نمایش درخت دودویی به وسیله ماتریس
در اين روش از یک ماتریس با سـه ستون كه ستون اول برچسب گره، ستون دوم شماره فرزند سمت چـپ و سـتون سـوم شـماره فرزند سمت راست است استفاده مي شود. تعداد سطرهای ماتریس به تعداد گره های درخت است. اين روش برای درخت های مورب، خلوت يا درخت هایی كه در مورد ساختار آنها اطلاعات کمی داریم می تواند روش مناسبی باشد. در اين روش، مقدار حافظه هدر رفته به تعداد گره ها بستگي دارد و از ساختار درخت مستقل اسـت. اگـر درخـت n گـره داشته باشد، ماتريس آن n +1 صفر دارد كه همان فضاي هدر رفته است.
برای نمایش درختی مثل درخت بالا از ماتریس زیر استفاده می کنیم.
|
فرزند راست |
فرزند چپ | گره | |
|
3 |
2 | A | 1 |
| 0 | 4 | B |
2 |
|
0 |
5 | C |
3 |
|
7 |
6 | D | 4 |
|
8 |
0 | E |
5 |
|
0 |
0 | F | 6 |
| 0 | 9 | G |
7 |
| 0 | 0 |
H |
8 |
| 0 | 0 | I |
9 |







دیدگاهتان را بنویسید
برای نوشتن دیدگاه باید وارد بشوید.