در بخش اول، دستور if گفته شد. برای دستور if، عبارت شرط می تواند عملیات ساده ریاضی همانند بررسی کوچکتر، بزرگتر و یا برابر بودن باشد که در بخش اول مطرح شد. اما، برخی مواقع نیازمند بررسی مواردی چون ذات و ماهیت یک متغیر هستیم. می خواهیم بدانیم ورودی داده شده عدد است یا بردار و یا ماتریس، یا می خواهیم بدانیم ماتریس تهی است یا سطری و یا ستونی. برای مواردی از این قبیل متلب دستوراتی دارد که برای فهم این موارد به ما کمک می کند. در متلب ورودی ها می توانند عدد، حرف و حتی عبارات منطقی باشند. دستورات پیش رو از قبیل عبارات منطقی می باشند.

عبارات منطقی (Logical)

عبارات منطقی در متلب پاسخ 0 و یا 1 می دهند. این به این معنی می باشد که یا منطقی هست یا نیست و پاسخی بین 0 و 1 وجود ندارد.

عبارات منطقی برای بررسی ماهیت ماتریس

برای تعیین ماهیت ماتریس وارد شده از دستورات منطقی زیر استفاده می شود.

isempty

برای بررسی تهی بودن یک ماتریس از این دستور استفاده می شود. مثالی در زیر آورده شده است که در آن یک ماتریس تهی و غیر تهی با این دستور بررسی می شوند.

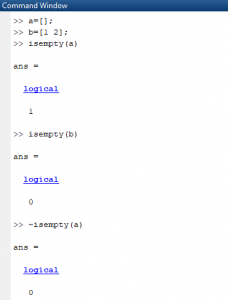
در ابتدا تهی بودن ماتریس a بررسی شد که پاسخ 1 بود به این معنی که a تهی است. برای ماتریس b پاسخ 0 بود. در دستور سوم با گذاشتن علامت ~ در سمت چپ عبارت، مخالف آن را اجرا می کنیم. در اینجا دستور سوم غیر تهی بودن a بررسی می شود. استفاده از ~ برای همه دستورات منطقی حاکم است.

isscalar

برای بررسی عدد بودن یک ورودی استفاده می شود. به عبارتی تشخیص می دهد که اندازه ماتریس و یا ورودی داده شده 1 در 1 است یا نیست.

isvector

برای بررسی بردار بودن یک ورودی استفاده می شود. بردار یک ماتریس یک بعدی می باشد به این معنی که تعداد یکی از سطر و یا ستون آن 1 می باشد. برای بررسی سطری و افقی بودن یک بردار می توان از دستور isrow و ستونی و یا عمودی بودن آن از دستور iscolumn استفاده کرد.

ismatrix

برای بررسی دو بعدی بودن ماتریس استفاده می شود. ماتریس های سه بعدی علاوه بر سطر و ستون شامل بعد سوم نیز می باشند اما ماتریس های دو بعدی فقط سطر و ستون دارند. توجه شود که این دستور ماتریس های تهی و برادارها را نیز در بر می گیرد.

برای بررسی ساختار درایه های ماتریس دستوراتی موجود هستند. برای بررسی قطری بودن ماتریس می توان از دستور isdiag و برای بررسی متقارن بودن از دستور issymmetric استفاده نمود. دستورات istril و istriu به ترتیب برای تشخیص پایین مثلثی یا بالا مثلثی بودن ماتریس می باشند. بالا مثلثی و یا پایین مثلثی بودن ماتریس در روش های حل ماتریسی مانند گاوس مهم می باشند. با استفاده از این دو روش منطقی می توان از حل، اطمینان حاصل نمود.

issorted

مرتب بودن ماتریس از نظر عددی می تواند مهم باشد. این دستور مرتب بودن ماتریس را از نظر عددی و کلاس بندی بررسی می کند. در این جا به مرتب سازی عددی اشاره می شود.

clc
clear
a=[12 3 4 5 7 8;0 -5 6 9 3 4;18 6 6 7 9 3]
b=sort(a,2,'ascend')
b_ascend_column=issorted(b,1,'ascend')
b_ascend_row=issorted(b,2,'ascend')
b_descend_row=issorted(b,2,'descend')

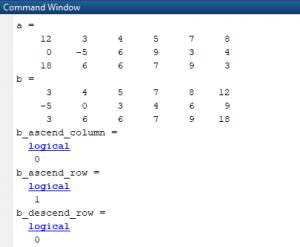
در مثال بالا در ابتدا یک ماتریس a وارد شد و سپس با دستور sort به صورت ردیفی و صعودی مرتب گردید. عبارت منطقی issorted به سه صورت استفاده شد. در حالت اول صعودی بودن ستون ها، حالت دوم صعودی بودن سطرها و در نهایت نزولی بودن سطرها بررسی گردید. مشاهده می شود که فقط برای حالت دوم پاسخ 1 می باشد.

بررسی عددها در ماتریس

ماتریس ها برای حل معادلات و معرفی سیستم ها به کار می روند. تشخیص ماهیت برخی عدد و درایه ها برای ما حائز اهمیت می باشد. برای مثال برخی از این دستوارت شامل isprime، برای تشخیص اول بودن و isreal برای تشخیص حقیقی بودن یک عدد یا داریه می باشند. دستور isnan برای تشخیص درایه های تعریف نشده می باشد. برای مثال، اگر عددی تقسیم بر صفر شود، پاسخ تعریف نشده است و متلب به صورت NaN نشان می دهد که به معنی این یک عدد نیست (Not a Number) می باشد. isfinite برای تعیین درایه های محدود استفاده می شود. اگر مخالف این دستور به کار برده شود، درایه های بی نهایت مشخص می گردند. در ادامه مثالی از isnan دیده می شود.

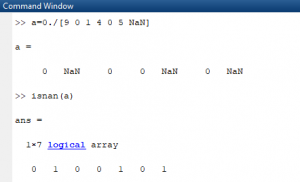
به دلیل ماتریسی بودن a، پاسخ دستور به صورت ماتریسی بوده و درایه های آن نظیر به نظیر در پاسخ به درایه های a می باشد.

بررسی برابری ماتریس ها

برای بررسی برابری ماتریس ها می توان از دو عبارت شرط استفاده نمود. isequal برای بررسی برابری ماتریس ها به صورت درایه به درایه و نظیر به نظیر می باشد. اما درایه NaN را بررسی نمی کند. isequaln دستور کامل تری از isequal می باشد و درایه های NaN را نیز بررسی می کند. در ادامه مثالی از isequaln مشاهده می شود.

clc
clear
a=[1 inf NaN 0 i]
b=[1 inf NaN 0 i]
c=[1 NaN 0 inf i]
isequal(a,b)
isequaln(a,b)
isequaln(a,c)

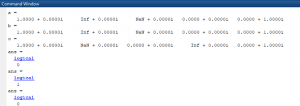
در مثال بالا دیده می شود که بردار c درایه های a و b را دارد اما به همان ترتیب نیست. به همین دلیل این دستور برابری a و c را 0 (خیر) اعلام میکند.

مثال

برنامه ای بنویسید که ساختار سلولی از کاربر بگیرد. اول تعیین کند ساختار سلولی هست یا خیر. در صورت سلولی بودن ورودی، بررسی کند که کدام دو درایه با هم برابر هستند و چه ماهیتی دارند (بردار یا ماتریس).

clc
clear
A=input('Please enter a cell structure: ')
nsc=1; nv=1; nm=1;
if iscell(A)
    for i=1:length(A)
        if isvector(A{i})
            v(nv)=i; nv=nv+1;
        elseif ismatrix(A{i})
            m(nm)=i; nm=nm+1;
        end
    end
    if length(v)>=2
        for i=1:length(v)/2
            for j=1:length(v)
                if j~=i
                    if isequal(A{v(i)},A{v(j)})
                        disp('equal Vectors')
                       equal_vectors=A{v(i)}
                       components_in_cell=[v(i) v(j)]
                    end
                end
            end
        end
    end
    if length(m)>=2
        for i=1:length(m)/2
            for j=1:length(m)
                if j~=i
                    if isequal(A{m(i)},A{m(j)})
                        disp('equal Matrices')
                        equal_matrices=A{m(i)}
                        components_in_cell=[m(i) m(j)]
                    end
                end
            end
        end
    end
else
    disp('you did not enter a cell structure')
end

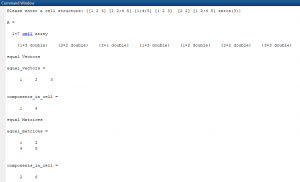
در مثال بالا در ابتدا ورودی از کاربر گرفته می شود. سپس بررسی می شود که ساختار سلولی هست یا خیر. در صورت بودن وارد شرط ها شده و در صورت نبودن نمایش می دهد که ساختار سلولی نیست. دو شرط برای بررسی بردار یا ماتریس بودن هر یک از درایه ها همراه با شمارنده موجود است. در صورتی که شمارنده عددی بزرگتر از 2 باشد، وارد حلقه های مقایسه شده و هر درایه را با درایه های دیگر مقایسه می کند و در صورت برابری، خود بردار یا ماتریس و جایگاهش را در ساختار سلولی اولیه نمایش می دهد.

در این مقاله دستورات منطقی مطرح شدند. دستوراتی برای تعیین ماهیت و ساختار ماتریس، ماهیت عدد و درایه های ماتریس و بررسی برابری ماتریس ها مطرح شدند. استفاده از این دستورات برای عبارت شرط if به صورت کاربردی آموزش داده شد. برای مقالات آینده حل معادلات و نامعادلات با متلب آموزش داده خواهند شد.